The Pythagorean identity tells us that no matter what the value of θ is, sin²θcos²θ is equal to 1 This follows from the Pythagorean theorem, which is why it's called the Pythagorean identity!Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16;Introduction to x plus y whole cube identity with example problems and proofs to learn how to derive xy whole cube formula in mathematics
Mechanically Resolved Imaging Of Bacteria Using Expansion Microscopy
Expand x 2 y 4 z whole square using suitable identity
Expand x 2 y 4 z whole square using suitable identity-Quotient of x^38x^217x6 with x3Binomial Theorem Formula The generalized formula for the pattern


Cbse 9 Math Cbse Polynomials Ncert Solutions
Solution (x 1)(x 1) can be written as (x 1) 2 Thus, it is of the form Identity I where a = x and b = 1 So we have, (x 1) 2 = (x) 2 2(x)(1) (1) 2 = x 2 2x 1 Example 2 Factorise (x 4 – 1) using standard algebraic identities Solution (x 4 – 1) is of the form Identity III where a = x 2 and b = 1 So we have, (x 4 – 1Apr 01, 17 · Use suitable identities to find the following products (i) (x 4) (x 10) (ii) (x 8) (x – 10) (iii) (3x 4) (3x – 5) (iv) (y 2 3 / 2) (y 2 – 3 / 2) (vIn mathematics, a square root of a number x is a number y such that y² = x;
In the algebraic identities for class 9, we will cover all the identities mentioned in the CBSE class 9 (NCERT) syllabus These algebraic identities basically carry variable equations in such a way, that the Lefthand side (LHS) of the equation is equal to its Righthand side(RHS)Click here👆to get an answer to your question ️ Expand each of the following, using suitable identities (2x y z)^2 Join / Login > 8th > Maths > Squares and Square Roots > Finding Square of a Number Find the square of the following numbers using the identity (aApr 05, 21 · A Computer Science portal for geeks It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions
X;y2R n The standard inner product between matrices is hX;Yi= Tr(XTY) = X i X j X ijY ij where X;Y 2Rm n Notation Here, Rm nis the space of real m nmatricesTr(Z) is the trace of a real squareOct 19, · The volume an ice cream cone that is given by the solid above \(z = \sqrt{(x^2 y^2)}\) and below \(z^2 x^2 y^2 = z\) The following problems examine Mount Holly in the state of Michigan Mount Holly is a landfill that was converted into a ski resortSign up to read all wikis and quizzes in math, science, and engineering topics



How To Expand Using The Identity A B C 2 B2 C2 2ab 2bc 2ca Youtube



Covid 19 Cases And Transmission In 17 K 12 Schools Wood County Wisconsin August 31 November 29 Mmwr
Access TopperLearning's free Selina Solutions for ICSE Class 9 Mathematics Chapter 4 Expansion to learn about finding the square of a given algebraic expression using expansion Also, go through the solutions to understand expansion of cubes Highlyexperienced Maths experts have created the answers for textbook exercises in a stepwise format to help it easy for students toCalculator Use This is a factoring calculator if specifically for the factorization of the difference of two squares If the input equation can be put in the form of a 2 b 2 it will be factored The work for the solution will be shown for factoring out any greatest common factors then calculating a difference of 2 squares using the idenityExample 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2 2·2·5 (2a) 2 = (5 2a) 2 Consequences of the above formulas



Expand 2 X 5 Y 3 Z Whole Square Using Suitable Identity Brainly In
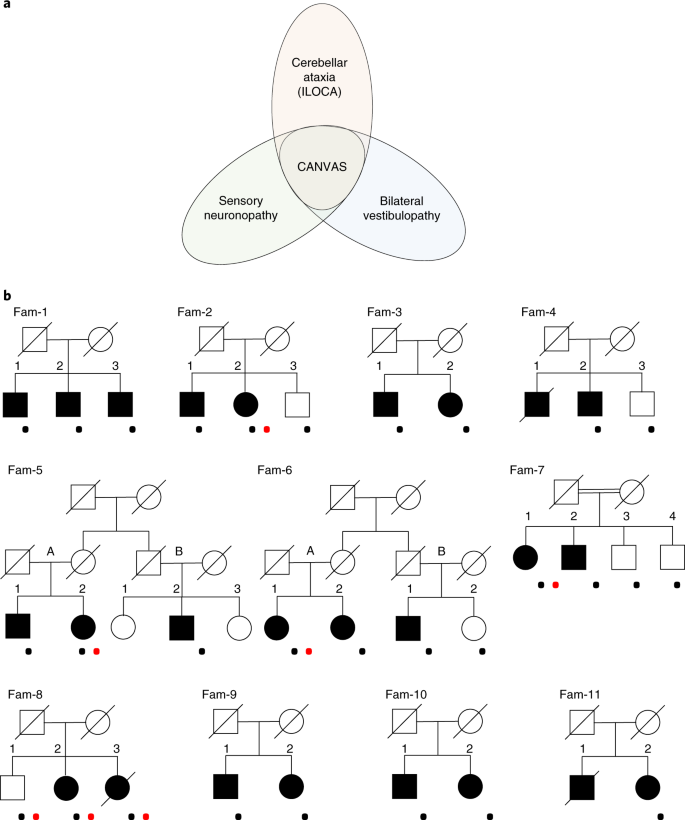


Biallelic Expansion Of An Intronic Repeat In Rfc1 Is A Common Cause Of Late Onset Ataxia Nature Genetics
That is, given two signals x 1(t) and x 2(t) and two complex numbers a and b, then ax 1(t) bx 2(t) ,aX 1(j!) bX 2The standard question you often get in your algebra classes they'll give you this equation and it'll say identify the conic section and then graph it if you can and the equation they give you won't be in the standard form because if it was you could just kind of pattern match with what I showed in some of the previous videos and you'll be able to get it so let's do a question like that and letJan 30, 18 · Expand using suitable identity (2x 5y 3z) to the whole square asked Sep 13, polynomials 0 votes 1 answer Expand (1/x y/3) whole cube asked Sep 14, 18 in Class XI Maths by navnit40 (4,939 points) polynomials 0 votes 1 answer If the zeroes of the quadratic polynomial xz (a 1)* b are 2 and 3, then (square) b



Ex 2 5 4 Expand Each Of The Following Using Suitable


Perform Symbolic Computations Matlab Simulink
In Algebra In Algebra putting two things next to each other usually means to multiply So 3(ab) means to multiply 3 by (ab) Here is an example of expanding, using variables a, b and c instead of numbers And here is another example involving some numbers112 Examples The standard inner product is hx;yi= xTy= X x iy i;318 Chapter 4 Fourier Series and Integrals Zero comes quickly if we integrate cosmxdx = sinmx m π 0 =0−0 So we use this Product of sines sinnx sinkx= 1 2 cos(n−k)x− 1 2 cos(nk)x (4) Integrating cosmx with m = n−k and m = nk proves orthogonality of the sines


Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z 2 Sarthaks Econnect Largest Online Education Community



Unexpected Conservation And Global Transmission Of Agrobacterial Virulence Plasmids Science
We can use this identity to solve various problemsA complex number z = x yi will lie on the unit circle when x 2 y 2 = 1 Some examples, besides 1, –1, i, and –1 are ±√2/2 ± i√2/2, where the pluses and minuses can be taken in any order They are the four points at the intersections of the diagonal lines y = x and y = x with the unit circle We'll see them later as square roots ofUse convenient identities for simplification, specified as the commaseparated pair consisting of 'IgnoreAnalyticConstraints' and true or false Setting 'IgnoreAnalyticConstraints' to true can give you simpler solutions, which could lead to results not generally valid In other words, this option applies mathematical identities that are convenient, but the results might not hold for all



Cambridge International As And A Level Mathematics Pure Mathematics 2 And 3 By Ayman Alam Issuu


Cbse 9 Math Cbse Polynomials Ncert Solutions
Click here👆to get an answer to your question ️ Expand each of the following, using suitable identities ( 2x 3y 2z)^2 Join / Login Find the square of the following numbers using the identity (a b) 2 = a 2 2 a b b 2 5 1 0 Medium View solution Find the square of the following number The Fish Tale Across the WallEnter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask about factoring factor quadratic x^27x12;Get FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 25 We have created Step by Step solutions for Class 9 maths to help you to revise



Example 19 Write 3a 4b 5c 2 In Expanded Form Examples



What Is The Formula For A B 4 Quora
Hint Consider f (x) = x 2 4 y x y 2 − 1 as a quadratic in x, where y is constant By Vieta its roots x , x ′ satisfy x x ′ = − 4 y Thus if x is a root then so too∇2f(x,y,z) = 02∇(xy z)·∇(x−2z) = 2(ij k)·(i−2k) = 2(10−2) = −2 This example may be checked by expanding (x y z)(x − 2z) and directly calculating the Laplacian Exercise 4 Use this rule to calculate the Laplacian of the scalar fields given below (click onMay 21, 21 · An algebraic identity is an equality that holds for any values of its variables For example, the identity
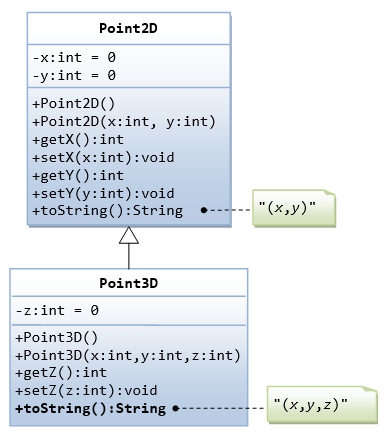


Oop Inheritance Polymorphism Java Programming Tutorial


Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Sarthaks Econnect Largest Online Education Community
Free trigonometric simplification calculator Simplify trigonometric expressions to their simplest form stepbystepJul 14, 18 · Find an answer to your question expand by using identity (2x y z)^2 shubham5616 shubham5616 Math Secondary School answered Expand by using identity (2x y z)^2 2 See answers gaurav13c gaurav13c MarkAsBrainliest MarkAsBrainliest WeDec 23, 17 · Expand the following (2xyz)the whole raised to 2 Share with your friends Share 0



Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education



Expand Using Suitable Identity 2x 5y 3z Sq Brainly In
May 24, 21 Algebraic Identities Polynomials, Class 9, Mathematics EduRev Notes is made by best teachers of Class 9 This document is highly rated byIn algebra, a nested radical is a radical expression (one containing a square root sign, cube root sign, etc) that contains (nests) another radical expression Examples include , which arises in discussing the regular pentagon, and more complicated ones such asMay 29, 18 · Transcript Example Expand (4a – 2b – 3c)2 (4a – 2b – 3c)2 = (4a (–2b) (–3c)) 2 Using (x y z)2 = x2 y2 z2 2xy 2yz 2zx Putting x = 4a



Ex 2 5 4 Expand Each Of The Following Using Suitable



Augmented Matrix An Overview Sciencedirect Topics
Expand following, using suitable identities (x 2y 4z)^2 CBSE CBSE (English Medium) Class 9 Textbook Solutions 50 Important Solutions 1 Question Bank Solutions 7801 Concept Notes & Videos 2 Syllabus Advertisement Remove all ads Expand following, using suitable identities (x 2y 4z)^2 MathematicsA 2 b 2 c 2 118 – 118 = 625 – 118 subtracting 118 from both the sides Therefore, a 2 b 2 c 2 = 507 Thus, the formula of square of a trinomial will help us to expand 7th Grade Math Problems 8th Grade Math Practice From Square of a Trinomial to HOME PAGEHowever, for quite some time Pascal's Triangle had been well known as a way to expand binomials (Ironically enough, Pascal of the 17th century was not the first person to know about Pascal's 3 = x 3 3x 2 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;


Expand The Following 4a B 2c 2 Studyrankersonline



Learning From Nature To Expand The Genetic Code Trends In Biotechnology
Now since z 1 ⁄ 2 = e 1 ⁄ 2 Log z, on the contour outside the branch cut, we have gained 2 π in argument along γ (By Euler's identity, e iπ represents the unit vector, which therefore has π as its log This π is what is meant by the argument of z The coefficient of 1 / 2 forces us to use 2 π) SoJan 24, 18 · You can't, really While it looks like you can just cancel out the squares with the square root, this only works if you have one square within the radical Since we're adding two together, it's slightly different There's no way to factor x^2y^2 to get a perfect square The only real way to simplify this expression is by using math that's at a higher than algebra level, so forLinearity Linear combination of two signals x 1(t) and x 2(t) is a signal of the form ax 1(t) bx 2(t) Linearity Theorem The Fourier transform is linear;



Effect Of Internationally Imported Cases On Internal Spread Of Covid 19 A Mathematical Modelling Study The Lancet Public Health



Using The Binomial Theorem College Algebra
Download free PDF of best NCERT Solutions , Class 8, Math, CBSE Algebraic Expressions and Identities All NCERT textbook questions have been solved by our expert teachers You can also get free sample papers, Notes, Important QuestionsIn other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x For example, 4 and −4 are square roots of 16, because 4² = (−4)² = 16 Every nonnegative real number x has a unique nonnegative square root, called theMar 29, · Definition binomial A binomial is an algebraic expression containing 2 terms For example, (x y) is a binomial We sometimes need to expand binomials as follows (a b) 0 = 1(a b) 1 = a b(a b) 2 = a 2 2ab b 2(a b) 3 = a 3 3a 2 b 3ab 2 b 3(a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4(a b) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5Clearly,



Expand Using The Identity A 2x 3y Z 2 Brainly In



Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver
Z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions They could equally well be be done using exponentials, for instance (assuming a6= b) Z cos(ax)cos(bx)dx= Z 1 2 (eiax e iax) 1 2 (eibx e ibx)dx = 1 4 Z (ei(ab)x ei(a b)x e i(a b)x e i(ab)x)dx = 1 2 Z (cos((a b)x) cos((a b)x))dx = 1 2Expand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce functionIntroduction to special product of binomials xa and xb and proofs of expansion of (xa)(xb) with example to learn how to use it in mathematics



Expand And Simplify Binomial Squares 2x 3y 2 Youtube


Covid Economics Centre For Economic Policy Research
Jan 30, 18 · Using suitable identity, evaluate the following (i) 103 3 (ii) 101 x 102 (iii) 999 2 Firstly adjust the given number into two number such that one is a multiple of 10 and use the proper identityMar 16, 17 · Ex 25, 4 Expand each of the following, using suitable identities (x 2y 4z)2 (x 2y 4z)2 Using (a b c)2 = a2 b2 c2 2ab 2bc 2ac Where a = x , b



Expand Each Of The Following Using Suitable Identities Ii 2x Y Z Brainly In


Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra



Ncert Exemplar Class 8 Maths Chapter 7 Algebraic Expressions Identities And Factorisation Learn Cbse



Using The Binomial Theorem College Algebra



Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra
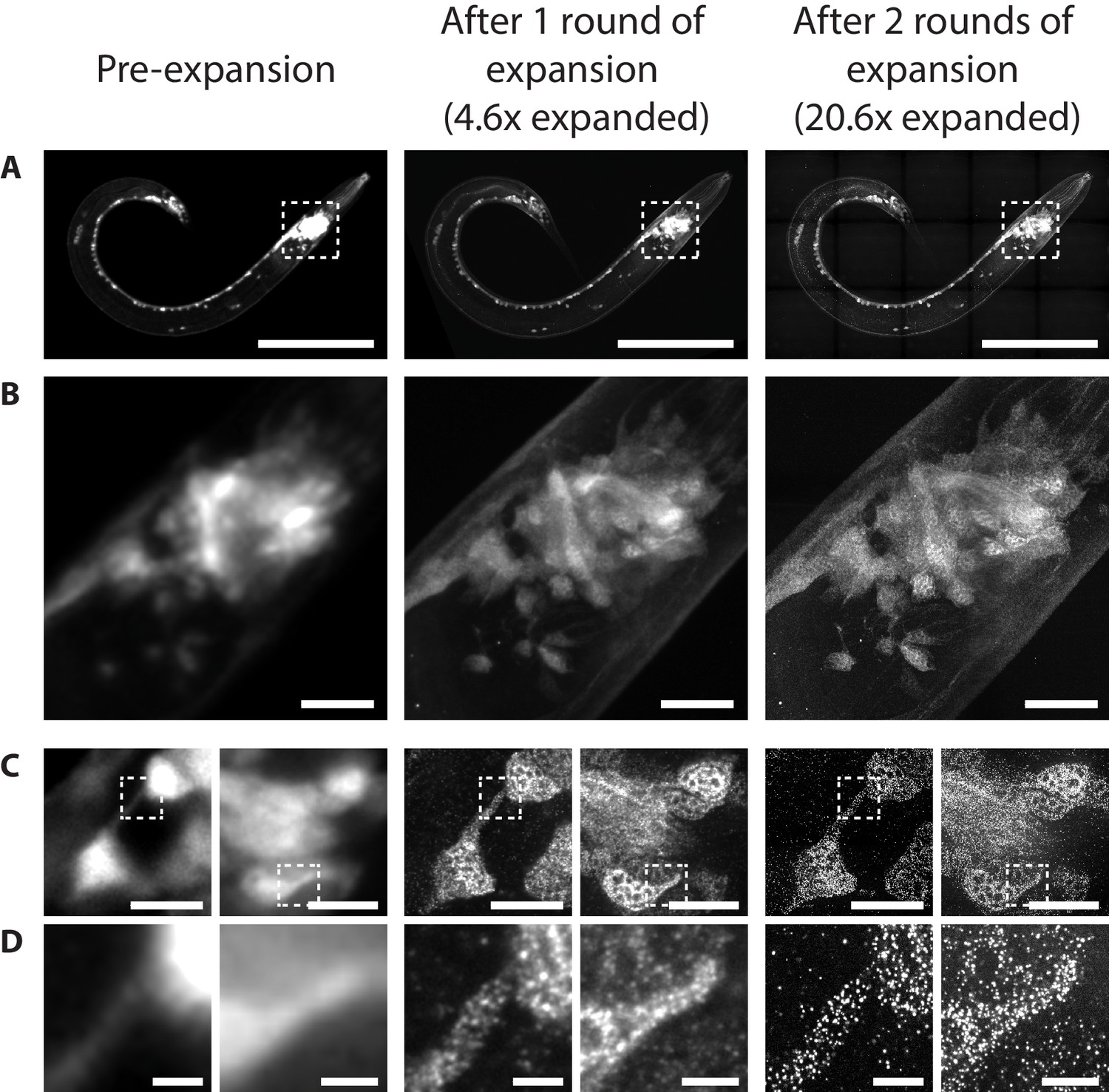


Expansion Microscopy Of C Elegans Elife



Partial Fractions Calculator Wolfram Alpha



Expand The Following 4a B 2c 2



Crystals Free Full Text Borates Crystal Structures Of Prospective Nonlinear Optical Materials High Anisotropy Of The Thermal Expansion Caused By Anharmonic Atomic Vibrations Html



Expand Each Of The Following Using Suitable Identities I X 2y 4z Square Brainly In
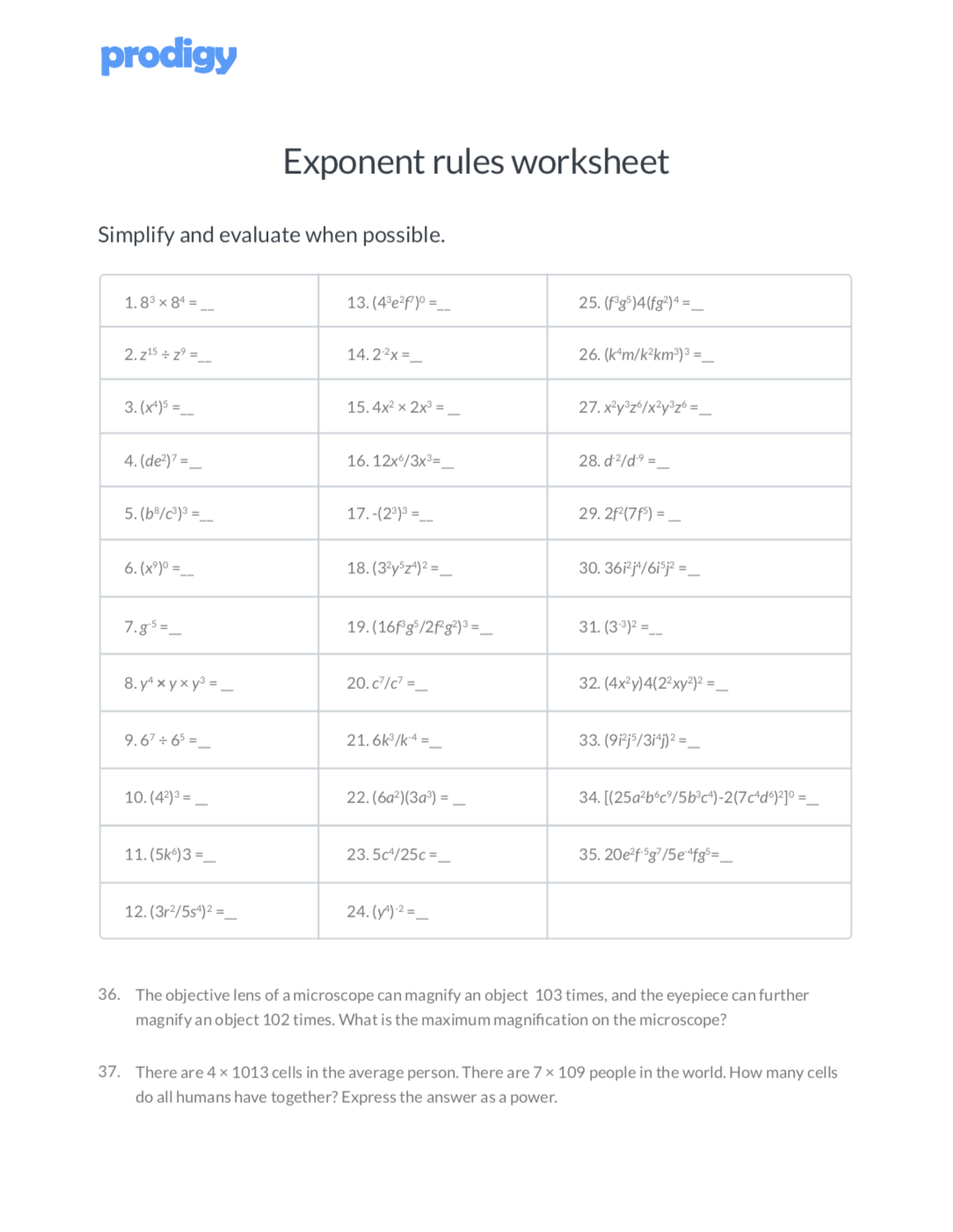


Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education



Expand Each Of The Following Using Suitable Identities X 2y 4z 2 2x Y Z 2 2x 3y 2z 2 Youtube


Cbse 9 Math Cbse Polynomials Ncert Solutions



Binomial Theorem Wikipedia



X 2y 4z Expand It Using Suitable Identities


What Is The Formula For A B C Quora



Ex 2 5 4 Expand Each Of The Following Using Suitable



A 4 B 2 1 2 Expand It With Suitable Identites Brainly In



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium
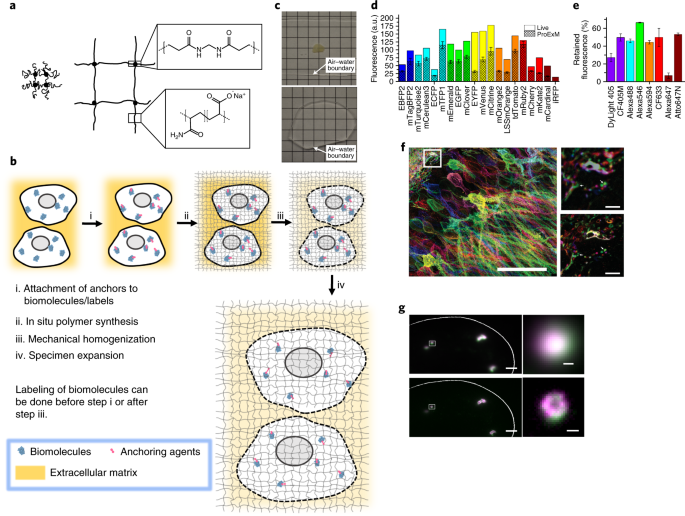


Expansion Microscopy Principles And Uses In Biological Research Nature Methods


Cbse 9 Math Cbse Polynomials Ncert Solutions


How To Solve For X And Y In X Y 5 And Xy 6 Quora



Rise 9 X Whole Square Minus 12 X Minus Y Square Minus Z Cute766



Binomial Theorem Wikipedia



X 2 3 Y Expand It Using Suitable Identities Brainly In
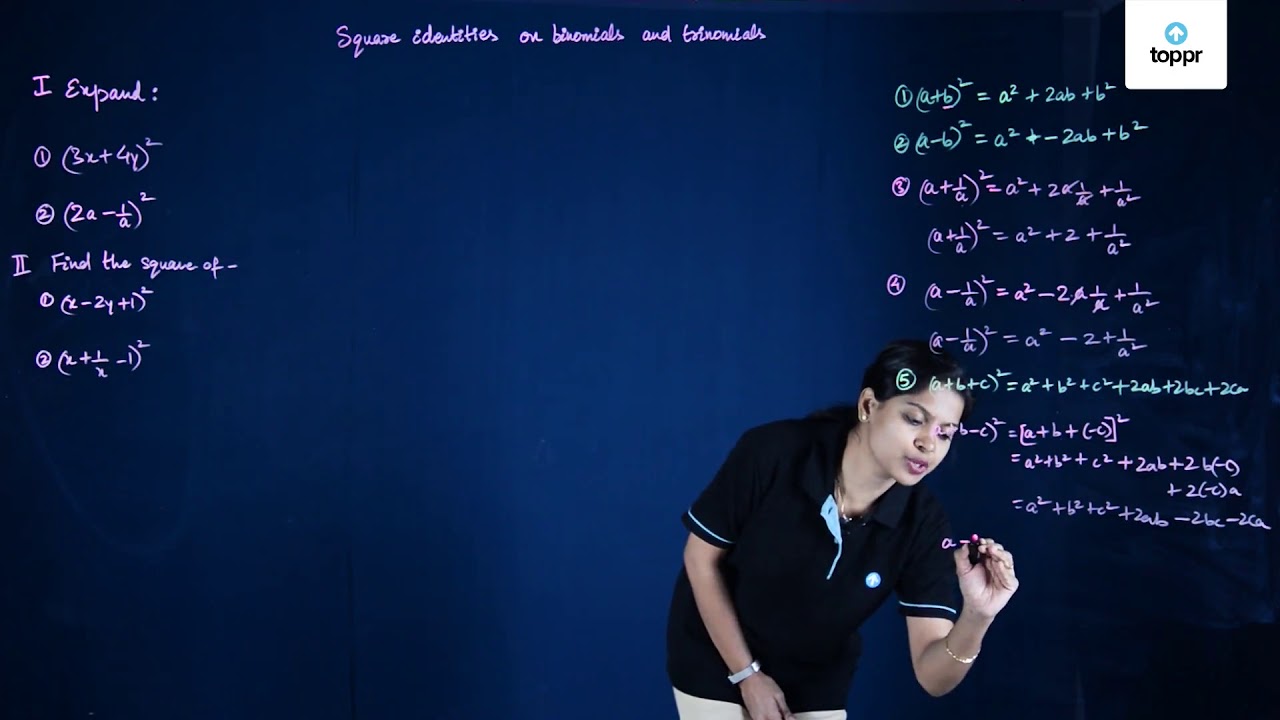


Standard Identities Of Binomials And Trinomials Equations Examples



Expand Using Suitable Identities X 2y 4z 2 2 3a 7b C 2 Brainly In


How Did Urban Land Expand In China Between 1992 And 15 A Multi Scale Landscape Analysis



Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



Square Algebra Wikipedia



Simplify Polynomial Rational Terms With Step By Step Math Problem Solver


Mechanically Resolved Imaging Of Bacteria Using Expansion Microscopy



Algebraic Identities Of Polynomials A Plus Topper



Pascal S Triangle And The Coefficients In The Expansion Of Binomials Ck 12 Foundation



Ex 9 5 3 Find The Squares By Using Identities I B 7 2
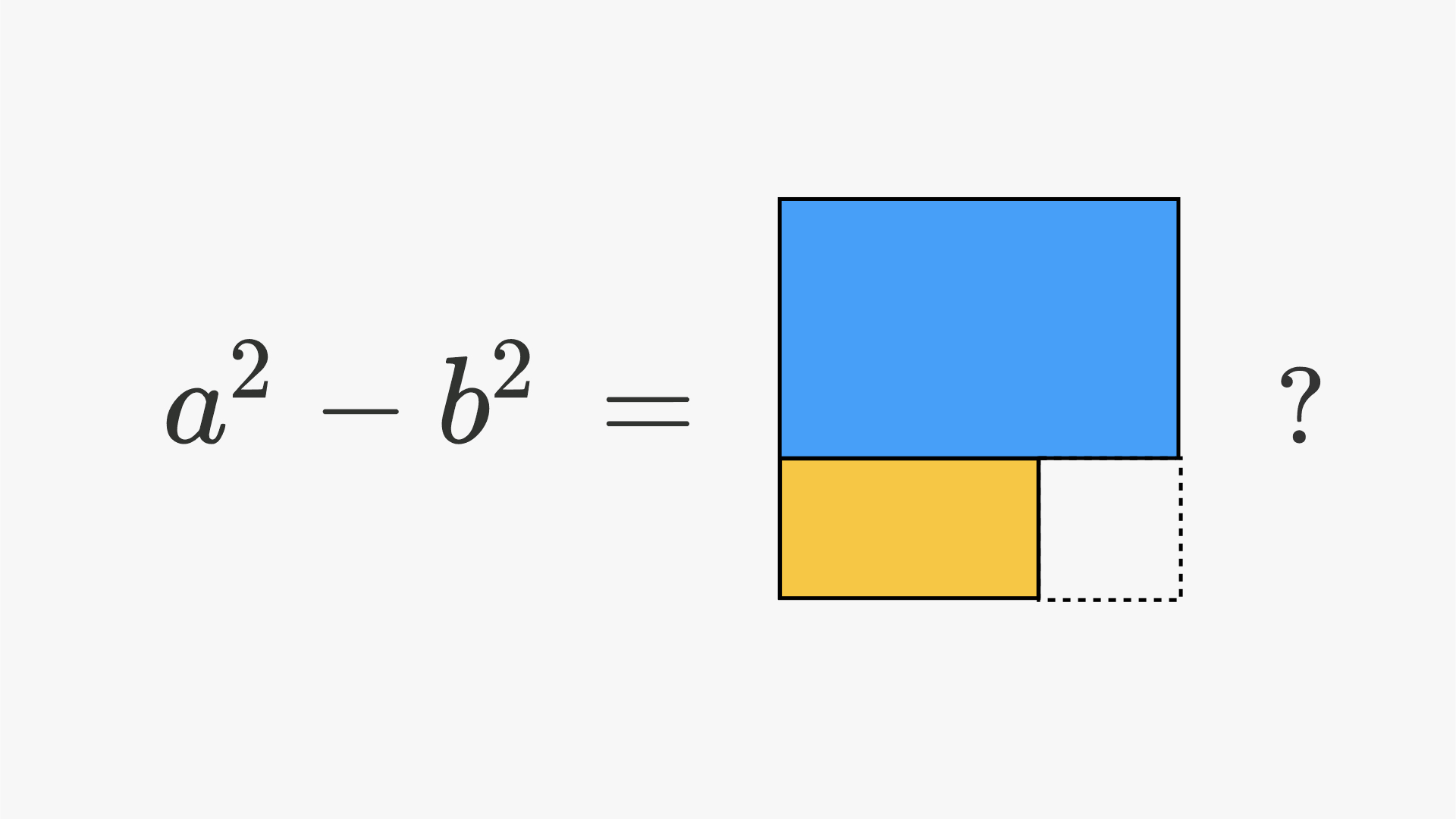


Difference Of Squares Brilliant Math Science Wiki


Indices And Logarithms



8 8 Taylor Series Mathematics Libretexts


Expand The Following 3a 2b 3 Studyrankersonline



Expand And Simplify Binomial Squares 2x 3y 2 Youtube



Square Algebra Wikipedia



Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z 2 Ii Youtube


X 2y 4z Expand It Using Suitable Identities



Expand Each Of The Following Using Suitable Identity I X 2y 4z Ii 2x Y Z Iii Brainly In



Factoring Using The Difference Of Squares Pattern Video Khan Academy
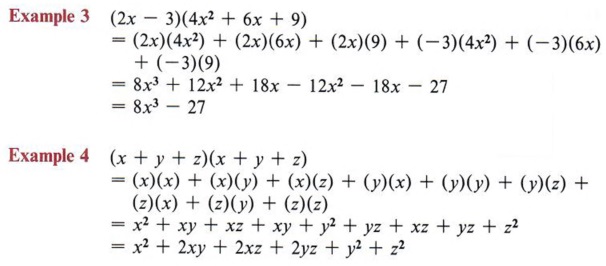


Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



Expanding Binomials Video Polynomials Khan Academy



Standard Identities Of Binomials And Trinomials Equations Examples
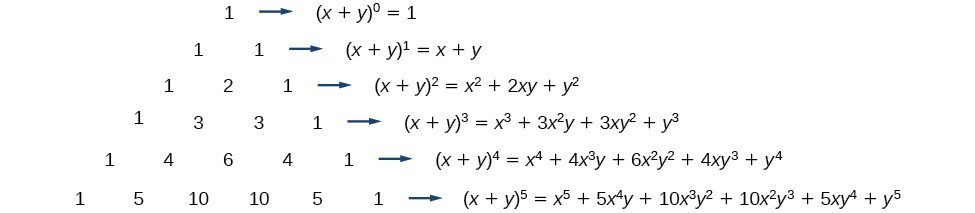


Using The Binomial Theorem College Algebra



Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube



Expand Each Of The Following Using Suitable Identities X 2y 4z 2 2x Y Z 2 2x 3y 2z 2 Youtube



0 件のコメント:
コメントを投稿